4 – Correzione dei diottri oculari ametropi

In questo paragrafo affronteremo le possibilità di trasformare  i diottri oculare ametropi  per renderli emmetropi, o meglio il più possibile vicini all’emmetropia. In questo capitolo il l’argomento è affrontato solo dal punto di vista teorico fisico, rimandiamo ai successivi capitoli la parte pratica e applicativa.

4.1 – Meccanismi e tecniche per emmetropizzare il diottro oculare ametrope

Per modificare un diottro oculare ametrope si può agire o sui vari fattori ametropizzanti oppure sostituendo o sottraendo un elemento del diottro. Inoltre, per ottenere un risultato analogo, è possibile aggiungere un sistema ottico per modificare il potere totale del diottro oculare.

Certamente alcune di queste tecniche sono puramente teoriche, per cui saranno poco approfondite, altre sono di natura chirurgica, per cui rimandiamo a testi specifici, altre, invece, sono puramente ottiche e saranno esposte più' approfonditamente.

• Agire sui fattori ametropizzanti

• Modificare la lunghezza del bulbo

 La modificazione della lunghezza del bulbo è una tecnica teorica di tipo chirurgico, che comporta una serie di ostacoli per l'applicazione pratica. In teoria una resezione sclerale permetterebbe un accorciamento del bulbo e una riduzione della miopia. Inoltre è molto grossolana ed applicabile solo alle miopie elevate.

Modificare la refrazione del diottro

La refrazione del diottro può essere modificata cambiando la curvatura corneale o l'indice di rifrazione di uno dei mezzi refrattivi.

Curvatura corneale 

Nella miopia, la modifica della curvatura corneale chirurgica o parachirurgica è molto diffusa e permette di avere risultati abbastanza soddisfacenti anche se con alcuni inconvenienti.

Tecnica chirurgica: cheratotomia radiale (incisioni radiali dalla zona periottica della cornea al limbus).

Tecnica parachirurgica:cheratectomia con laser a eccimeri (ablazione con il laser di tessuto corneale in zona ottica).

Nella ipermetropia, le tecniche chirurgiche e parachirurgiche sono meno usate perché presentano risultali minori e necessitano di tecniche più complesse.

Tecnica chirurgica: epicheratofachia (impianto sulla superfice corneale, dopo essere stata disepitelizzata, di un lenticolo positivo).

Tecnica parachirurgica: fotoablazione a corona in area prelimbare (tecnica ancora poco affidabile).

Indice di rifrazione

La modifica di uno degli indici di rifrazione del diottro oculare è ancora un metodo puramente teorico, che però potrebbe in futuro dare buoni risultati con tecniche chirurgiche semplici.

Sottrazione o sostituzione di un elemento del diottro

Questa tecnica è essenzialmente chirurgica e attualmente è applicata solo al cristallino e nella miopia elevata. Consiste nella asportazione del cristallino o nella sostituzione con un cristallino artificiale di potere minore, in modo tale da riportare il fuoco più vicino possibile alla retina.

Teoricamente può essere applicata anche nella ipermetropia, impiantando un cristallino artificiale con potere maggiore.

Aggiunta di un sistema ottico

Questo è il metodo più semplice e più antico di modificare la refrazione di un diottro oculare ametrope.

Anteponendo davanti al diottro oculare una o più lenti, positive o negative, è possibile riportare il fuoco sulla retina. Il potere delle lenti da anteporre dipende non solo dal potere del diottro oculare ma anche dalla distanza a cui vengono poste. In base a questa distanza possiamo distinguere:

Correzione refrattiva con lenti a contatto

(rimandiamo ai prossimi capitoli per ulteriori approfondimenti).

Correzione refrattiva con lenti su occhiali

 (sarà oggetto dei prossimi paragrafi)

4.2 – Le lenti in oculistica

Come abbiamo visto nella prima parte, le lenti possono essere sferiche concave, sferiche convesse, cilindriche, toriche, ecc.  In questo paragrafo cercheremo di approfondire le caratteristiche geometriche, fisiche e teoriche di tutte le lenti utili all’oftalmologo per modificare il diottro oculare ametrope e per portarlo all’emmetropia.

È da ricordare, come precedentemente esposto nel primo capitolo, che le lenti convesse hanno un potere diottrico positivo, cioè hanno il potere di convergere i raggi verso l’asse, mentre quelle concave hanno un potere diottrico negativo, cioè hanno il potere di divergere i raggi.

Caratteristiche geometrico-fisiche

Tutte le lenti possono essere considerate composte da una o più lenti semplici (sferiche  e cilindriche), queste a loro volta possono avere una  o entrambe le superfici rifrangenti con capacità diottriche. In pratica tutte le lenti usate in oftalmologia possono essere considerate una combinazione di una o più lenti semplici.

Le lenti semplici di base sono:

Lenti sferiche

Le lenti sferiche ( si abbrevia con sf) sono un sistema ottico formato da due superfici, di cui almeno una concava o convessa, che formano un diottro composto. In una lente sferica distinguiamo:

centro di curvatura (centro della sfe­ra di cui le superfici fanno parte);

rag­gio di cavatura (raggio della sfera);

asse ottico (linea che unisce i centri di curvatura delle due superfici)

punti coniugati (punto di origine e punto in cui convergono i raggi che attraversano la lente).

Il poter di una lente è espresso in diottrie (D), che è dato dalla somma algebrica dei poteri dei due diottri (anteriore, formato dalla prima superficie,  e posteriore, formato dalla seconda superficie) componenti la lente.

La lente sferica può essere:

convergente (vergenza positiva), con potere complessivo positivo, detta anche positiva; ha entrambi i fuochi reali e lo stesso potere rifrattivo in tutti gli assi. Questa lente viene descritta scrivendo il potere diottrico preceduto dal segno positivo, esempi: +1;  +2;  +3,5;  +4,25.

divergente (vergenza negativa), con potere complessivo negativo, detta anche negativa; ha entrambi i fuochi virtuali e lo stesso potere rifrattivo in tutti gli assi. Questa lente viene descritta scrivendo il potere diottrico preceduto dal segno negativo, esempi: ^_1;  ^_2;  ^_3,5;  ^_4,25.

Il potere complessivo della lente in diottrie è dato dalla formula:

                                                                 n₁ = indice di rifrazione del primo mezzo (aria)

 D =  (n₂ – n₁) (1/R₁ – 1/R₂)                      n₂ = indice di rifrazione del materiale della lente

                                                                  R₁ e R₂  =  Raggi di curvatura delle due superfici

Nel caso che una delle due superfici è piana, la formula si riduce a:

                                                         n₂ ^_  n₁
                                             D =  ^{_____________}   
                                                             R

Il fuoco della lente è

                                                    f  =  1/D

Per esempio una lente con le due superfici uguali convesse in cui R₁=R₂= 10 cm = 0,1 m, immersa nell’aria ( n = 1) e con indice di rifrazione n₂= 1,5  ,  avrà potere:

     D = (1,5 – 1) (1/0,1 + 1/0,1)  =  0,5 _*  20  =  10

 e fuoco 

     f = 1/10 =  0,1 m =  10 cm

Le due superfici delle lenti sferiche possono essere anche diverse tra loro: una concava e l’altra convessa, una curva e l’altra piana, ambedue concave o convesse. Esistono lenti biconvesse e biconcave in cui entrambe le superfici sono convesse o concave; le lenti piano-convesse e piano-concave sono formate da una superficie piana ed una convessa o con­cava;  le lenti sferiche concavo-convesse sono costituite dall'associazione di una superficie convessa con una concava, il potere di queste ultime sarà positivo o negativo secondo che se è maggiore il potere positivo o negativo

Per esempio una lente positiva di 3 diottrie può essere data da:

- una lente piano-convessa con una superficie convessa di 3 D;

- una lente concavo-convessa  con una superficie positiva di   +5 D e una superficie negativa di  –2 D, con somma algebrica di +3;

- una lente biconvessa con ambedue le superfici positive di 1,5 D, con somma algebrica di +3D.

Il potere diottrico di una lente indica anche la vergenza che imprime ai raggi passanti attraverso di essa. Dopo aver attraversato una lente sferica i raggi luminosi hanno una vergenza uguale alla somma algebrica della vergenza che avevano a prima della loro penetrazione  nella lente e della vergenza che la lente ha dato loro. Per esempio i raggi lu­minosi che provengono da una sorgente situata a 20 cm da una lente sferica + 5 D hanno, prima di penetrare nella lente, una vergenza negativa di 5 D (perché la sorgente si trova a 20 cm e la vergenza è data dall’inverso della distanza), per cui la lente positiva di 5 D annulla la vergenza ne­gativa iniziale e i raggi fuoriescono paralleli dalla lente. Se la lente in esame avesse un potere di 10, i raggi uscirebbero con una vergenza residua positiva di 5 D, per cui con convergerebbero su un fuoco posto a 20 cm.

Riassumendo possiamo dire che:

il poter di una lente indica la capacità di convergere o divergere (vergenza positiva o negativa) i raggi;

il fuoco di una lente è dato dall’inverso del poter diottrico (1/D);

una lente fornisce una vergenza ai raggi che la attraversano, data dal potere diottrico

i  raggi provenienti da una sorgente hanno una vergenza, anch’essa indicata in diottrie, che è data dall’inverso della distanza della sorgente (1/d)

i raggi che attraversano una o più lenti escono con una vergenza positiva o negativa data dalla somma algebrica della vergenza iniziale e di quella data dalle lenti che attraversano;

i raggi paralleli hanno una vergenza nulla

i raggi convergenti hanno un fuoco reale, quelli divergenti un fuoco virtuale;

i raggi visti attraverso una lente sembrano provenire da una distanza data dall’inverso della vergenza risultante dopo l’attraversamento.

Come abbiamo visto nel primo capitolo le lenti positive danno una immagine reale e capovolta se l'oggetto è situato al di là  fuoco principale ed una immagine virtuale e diritta quan­do l'oggetto è situato tra la lente e il fuoco princi­pale. Le lenti negative dannosempre una imma­gine virtuale e diritta.

Lenti cilindriche

Le lenti cilindriche (chiamate anche cilindri e abbreviate con cil) sono un sistema ottico formato da due superfici, di cui almeno una costituita da una superficie cilindrica o torica concava o convessa, che formano un diottro composto.

Mentre le lenti sferiche hanno una curvatura uguale su tutti i meridiani, quelle cilindriche hanno una curvatura variabile nelle varie sezioni: è massima in corrispondenza della sezione tra­sversale all’asse del cilindro, mentre in corrispondenza della sezio­ne longitudinale la curvatura è assente,  nelle sezioni intermedie fra queste due la curvatura varia in modo progressivo. In tal modo varia anche il potere diottrico della lente, cresce progressivamente da zero fino al potere massimo. Il potere in diottrie di una lente cilindrica di un potere conosciuto (D) su un meridiano posto ad un angolo a dal suo asse può essere calcolato con la formula:

                                                       D_a  =  D sin² a

In una lente cilindrica la somma dei poteri su assi perpendicolari è sempre uguale al potere totale del cilindro.

In una lente cilindrica distinguiamo:

-         rag­gio di cavatura (variabile per ogni sezione: da un minimo, che corrisponde al raggio di curvatura della sezione con curvatura massima, fino all’infinito, corrispondente alla sezione con curvatura nulla);

-         centro di curvatura (variabile in base al raggio);

-         asse del cilindro (meridiano in cor­rispondenza del quale la curvatura è assente);

-         linea focale (linea in cui convergono i raggi paralleli che passano per la lente);

-         meridiano del potere (meridiano perpendi­colare all'asse del cilindro)

Il potere in diottrie di una lente cilindrica è dato dall'inverso della distanza in metri che separa la linea focale dal­la lente.

Le lenti cilin­driche vengono dette anche lenti astigmatiche, questo termine deriva dal greco:

a (alfa negativo), stigma = punto  à  senza punto focale.

L’effetto delle lenti cilindriche dipende anche dal loro asse, la posizione di questo è data in gradi, per cui è necessario stabilire una convenzione, valida per tutti, per indicarla senza errore. Esistono due sistemi possibili per indicare la posizione dello zero nella misurazione dei gradi dell’asse del cilindro:

sistema internazionale (lo zero è sul meridiano orizzontale in corrispondenza del naso del paziente, quindi a destra dell’esaminatore per l’occhio destro del paziente, a sinistra dell’esaminatore per l’occhio sinistro del paziente);

sistema TABO (lo zero è sempre a destra dell’esaminatore).

Come per le lenti sferiche, anche per quelle cilindriche le due superfici della lente possono essere diverse tra loro: una cilindro-concava e l’altra cilindro-convessa, una curva e l’altra piana, ambedue cilindro-concave o cilindro-convesse. Esistono lenti cilindriche biconvesse e biconcave in cui entrambe le superfici sono cilindri convessi o concavi; le lenti piano-convesse e piano-concave sono formate da una superficie piana ed una cilindro-convessa o cilindro-con­cava;  le lenti sferiche cilindriche concavo-convesse sono costituite dall'associazione di una superficie cilindro-convessa con una cilindro-concava, il potere di queste ultime sarà positivo o negativo secondo che se è maggiore il potere positivo o negativo. I due cilindri che formano le due superfici possono avere lo steeso asse, asse perpendicolare, oppure gli assi possono essere obliqui tra loro.

Per esempio una lente positiva di 3 diottrie può essere data da:

- una lente piano-cilindro-convessa con una superficie cilindro-convessa di 3 D;

- una lente cilindro-concavo-cilindro-convessa  con una superficie positiva di   +5 D e una superficie negativa di  –2 D, con asse uguale,  somma algebrica di +3;

- una lente biconvessa con ambedue le superfici positive di 1,5 D, con asse uguale, somma algebrica di +3D.

Nel caso che i cilindri delle due superfici non hanno lo stesso asse, i calcoli si complicano, perché è necessario applicare la formula per il calcolo del potere nella sezione diversa da quella ortogonale all’asse; poiché lenti di questo tipo non sono usate comunemente dall’oftalmologo, è opportuno tralasciarne il calcolo.

Le lenti cilindriche sono descritte in modo completo dal potere diottrico preceduto dal segno positivo o negativo, se convesse o concave, e seguito dall’indicazione in gradi dell’asse, esempi: +1(90°);  ^_2(180°);  +3,5(120°);  ^_4,25(70°). 

Combinazione delle lenti

Combinazioni tra lenti sferiche

Combinazioni tra sole sfere determinano un nuovo sistema  sferico, il cui potere è dato dalla somma algebrica dei poteri delle lenti.

Esempio di combinazione tra sfere:  + 1 sf  e +3 sf  à  +4 sf

Combinazioni tra lenti cilindriche

Combinazioni tra soli cilindri con asse uguale:

determinano un nuovo sistema ottico equivalente ad un diottro cilindrico con asse uguale e con potere dato dalla somma algebrica dei poteri delle lenti.

Esempi:  + 2 (90°)  e  + 1 (90°)  à  +3 (90°)

               + 3 (180°)  e  -2 (180°)  à +1 (180°)

Combinazioni tra cilindri con potere e segno uguali ed assi ortogonali:

danno origine a un sistema ottico equivalente ad un diottro sferico con potere uguale al potere dei cilindri componenti il sistema.

Esempio:  +2 (180°)  e +2 (90°)  à   +2 sf

Combinazioni tra cilindri con potere uguale o diverso, segno diverso ed assi ortogonali: danno origine a un sistema ottico equivalente ad una combinazione sfero-cilindrica:

-         la sfera ha il potere e il segno di uno dei due cilindri originali

-         il cilindro ha l’altro segno, il potere dato dalla somma dei valori assoluti (cioè senza tenere conto del segno) dei poteri dei cilindri originali e l’asse uguale a quello del cilindro originale con lo stesso segno.

Esempi:  + 2 (180°)  e –3 (90°)  à  +2 sf  - 5 (90°)

Combinazioni tra cilindri con potere e segno uguali ed assi obliqui tra loro:

determinano un nuovo sistema ottico equivalente ad una combinazione sfero-cilindrica con sfera e cilindro dello stesso segno, l’asse del cilindro è posizionato in corrispondenza della bisettrice dell’angolo formato dagli assi dei cilindri obliqui; il  potere deve essere calcolato:

bisettrice ed asse del nuovo cilindro

 poere del cilindro

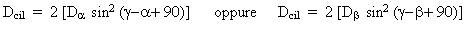
Combinazioni tra cilindri con potere diverso, segno uguale ed assi obliqui tra loro:

determinano un nuovo sistema ottico equivalente ad una combinazione sfero-cilindrica con sfera e cilindro dello stesso segno, l’asse del cilindro si trova nell’angolo formato d’incrociamento (formato dagli assi dei due cilindri originali) spostato verso il cilindro con potere maggiore in base alla seguente proporzione:

( i segni |  |  indicano il valore assoluto, quindi devono essere considerati senza il segno).

I poteri sono calcolati nel seguente modo:

sfera
D_sf  = D_a  sin² (g-a) + D_b  sin² (g-b)
cilindro
D_sf  = D_a  sin² (g-a+ 90) + D_b  sin² (g-b+90)

Combinazioni tra cilindri con potere uguale, segno diverso ed assi obliqui tra loro:

determinano un nuovo sistema ottico equivalente ad una combinazione tra due cilindri di segno diverso ed assi ortogonali, gli assi dei cilindri sono al di fuori dell’angolo d’incrociamento, equidistanti 45° dalla bisettrice dello stesso; il  potere deve essere calcolato:

nuovi assi

Combinazioni tra cilindri con potere diverso, segno diverso ed assi obliqui tra loro:

determinano un nuovo sistema ottico equivalente ad una combinazione tra due cilindri di segno diverso ed assi ortogonali (separati da un angolo di 90°), gli assi dei cilindri sono al di fuori dell’angolo d’incrociamento e distanti dalla bisettrice dello stesso in base alla seguente proporzione:

Combinazioni sfero-cilindriche

Se associamo una lente sferica ad una lente cilin­drica si crea un nuovo diottro in cui il po­tere nei vari meridiani è dato dalla somma algebrica dei poteri delle due lenti negli stessi meridiani. Nel meridiano dell'asse del cilindro il potere del nuovo sistema è uguale a quello della lente sferica, mentre nel meridiano perpendicolare all'asse del cilindro il potere è dato dalla somma algebrica del valore della lente cilindrica e di quella sferica.

Una combinazione sfero-cilindrica determina la formazione di due linee focali perpendicolari fra loro, quindi distinguiamo:

-         linea focale anteriore  (ha stessa direzione del meridiano di potere minore);

-         linea focale posteriore(ha stessa direzione del meridiano di potere maggiore);

-         intervallo o conoide di Sturm (struttura geometrica spaziale, formata dai raggi rifratti dalla combinazione sfero-cilindrica, compresa tra le due linee focali)

-         cerchio di minor confusione  (Sezione del conoide di Sturm in cui si ha la minor deformazione dell’immagine, è circolare);

-         equivalente sferico (media fra i poteri dei due meridiani principa­li di una combinazione sfero-cilindrica; l’inverso di questo potere corrisponde anche alla posizione del cerchio di minor confusone).

Più combinazioni sfe­ro-cilindriche con astigmatismi di valore molto diffe­rente possono avere lo stesso equivalente sferico, purché ad una differente lente cilin­drica corrisponda una lente sferica adeguatamente differente: la metà della differenza tra i cilindri deve essere uguale alla differenza tra le sfere. Per esempio il valore di 5 D può essere equivalente sferico delle seguenti combinazioni sfero-cilindriche:

-         +4sf  e +2cil (con poteri nei due assi di +4 e +6)

-         +3sf  e +4cil (con poteri nei due assi di +3 e +7)

-         +2sf  e +6cil (con poteri nei due assi di +2 e +8).

Se aggiungiamo una lente sferica ad una combina­zione sfero-cilindrica si modificano le dimensioni dell’intervallo di Sturm, ma si sposta la posizione  rispetto al diottro. L’aggiunta di una lente cilindrica modifica le dimensioni del conoide.

Nelle tabelle che seguono sono elencate tutte le lenti, con i rispettivi dati geometrico-fisico, che possono essere ottenute dalla combinazione delle suddette lenti semplici:

Trasposizione

Metodo

Dal punto di vista ottico-refrattivo è possibile ottenere combinazioni sfero-cilindriche sia con cilindri positivi che con cilin­dri negativi di potere uguale. Paretendo da una combinazione sfero-cilindrica , è possibile ottenere un sistema ottico equivalente con un cilindro di segno opposto ed uguale potere, ma con asse ortogonale, e modificando opportunamente la sfera..Il  potere della nuova lente sferica è dato dalla somma algebrica dei valori della sfera e del cilindro originari; il segno è lo stesso della sfera della combinazione di partenza. Questa metodo, detto trasposizione, è molto importante nella pratica dell’oftalmologo e nella prescrizione delle lenti.

In pratica per eseguire una corretta trasposizione è necessario eseguire con cura le seguenti fasi:

1)      cambiare di segno al cilindro (da + a – o da – a + );

2)      spostare di 90° l’asse del cilindro ( da 90° a 180° , da 180° a 90°, 30° a 120°, da 150° a 60°, ecc.)

3)      Il potere della nuova lente sferica è dato dalla somma algebrica del cilindro e della sfera della combinazione originaria;

4)      il segno della sfera è dato dalla somma algebrica del cilindro e della sfera originari, quindi se sono diversi prevale quello con potere maggiore.

Esempio di trasposizione della combinazione +1sf  +2 cil (90°):

1)      il cilindro diventa –2;

2)      l’asse del cilindro diventa (180°);

3)      la sfera è 3sf;

4)      il segno della sfera è +1 +2= +3 , cioè positivo;

quindi la nuova combinazione è + 3sf  –2 (180°).

Esempi: +3 +1 (150°)   à   +4 –1 (60°)

              –1 –2 (80°)      à   –3 +2 (170°)

              –1 +2 (90°)      à   +1 –2 (180°)   (il segno della sfera è dato da: -1+2 = +1, cioè +)

        –2  +2 (90°)     à   –2  (180)   (il potere della sfera è –2 +2 = 0)

Croce ottica

Il metodo della croce ottica è diventato di uso quotidiano per l’oftalmologo, permette di rendere più semplice la rappresentazione della refrazione di un diottro oculare e di facilitare l’applicazione della trasposizione e delle combinazioni tra lenti.

La croce ottica è una croce grafica che rappresenta, con i suoi due bracci, i due meridiani principali di un sistema ottico. Su ogni braccio vengono trascritti i valori in diottrie, con il segno positivo o negativo, della refrazione nel meridiano corrispondente e il valore in gradi dell’angolo formato dal meridiano con quello orizzontale (considerato il meridiano di riferimento):

      Rappresentazione con la croce ottica delle ametropie:

-         Ametropia sferica (miopia e ipermetropia)

à entrambi i meridiani uguali al potere della ametropia;

esempio: +2 sf                                                         

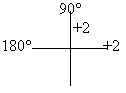
-         Ametropia astigmatica semplice (un meridiano emmetrope  ed uno miope o ipermetrope)     à il meridiano corrispondente all’asse del cilindro uguale a zero, il meridiano ortogonale con il potere del cilindro;

esempio: +2 cil (90°)                                              

-         Ametropia astigmatica composta (composta da una sfera e un cilindro, entrambi dello stesso segno (miope o ipermetrope)

      à il meridiano corrispondente all’asse del cilindro uguale al potere della sfera, il meridiano ortogonale con potere dato dalla somma della sfera e del cilindro;

esempio: +1 sf  +2 cil (90°)                                         

-         Ametropia astigmatica mista (con un asse miope ed uno ipermetrope, dato dalla combinazione di una sfera ed un cilindro di segno opposto

      à il meridiano corrispondente all’asse del cilindro uguale al potere della sfera, il meridiano ortogonale con potere dato dalla somma algebrica della sfera e del cilindro;

esempio: -1 sf  +3 cil (90°)                                             

Queste regole sono valide anche se gli assi dei meridiani non sono a 90° e 180° ma obliqui rispetto al meridiano orizzontale, però sempre ortogonali tra loro (esempio 70° e 160°):

esempio:   +1sf  +1 cil (140°)

Con la croce ottica è possibile annotare i ri­sultati della schiascopia (tecnica oggettiva di misurazione della refrazione che verrà esaminata nel prossimo capitolo). I valori segnati sulla croce ottica corrispondono alla refrazione per una correzione con occhiali, cioè per una correzione corrispondente alla distanza degli occhiali, perché per ogni distanza di correzione il potere della lente si modifica lievemente, come vedremo in seguito.

CONTINUA