| Ottica
oftalmica e fisiopatologia della refrazione Alfredo Parrozzani |
www.oculistanet.it |
4 - DIOTTRICA (Rifrazione della luce)
Un raggio luminoso che incontra la superficie di separazione di due mezzi trasparenti diversi 1 e 2, il raggio incidente dà luogo a un raggio nel secondo, chiamato raggio rifratto, che si propaga in una direzione diversa da quella del raggio incidente. Questo è il fenomeno della rifrazione della luce, di cui si occupa la diottrica. Si ha un raggio unico nel secondo mezzo, dopo la rifrazione, solo se il raggio incidente è monocromatico, cioè se in esso è presente luce di un solo colore. Quindi nello studio della rifrazione supponiamo che sia realizzata questa condizione.

.1 - Leggi della rifrazione
L’angolo di rifrazione r è formato dal raggio rifratto con la normale alla superficie di separazione dei due mezzi nel punto di incidenza.
La rifrazione avviene rispettando le seguenti leggi di Snellius -Cartesio:
1) il raggio incidente, la normale alla superficie di separazione dei due mezzi nel punto di incidenza e il raggio rifratto giacciono nello stesso piano;
2) esiste un rapporto costante tra il seno dell'angolo di incidenza e il seno dell'angolo di rifrazione:
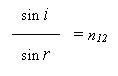
n12 è il valore costante del suddetto rapporto, ed è definito indice di rifrazione relativo del secondo mezzo rispetto al primo. Questo indice dipende unicamente dalla particolare coppia di mezzi considerati per un determinato colore della luce.
Se il secondo mezzo è otticamente più denso del primo si ha che il raggio rifratto nel secondo mezzo è più vicino alla normale di quanto lo è il raggio incidente, cioè l'angolo di rifrazione r è più piccolo dell'angolo di incidenza i; quindi essendo sin i> sin r sarà n12>1. Viceversa abbiamo che se i < r, cioè se sin i < sin r, sarà n12 < 1. In questo caso il secondo mezzo è meno rifrangente del primo.
Quindi è possibile affermare che un raggio luminoso che si rifrange passando da un mezzo meno rifrangente a un mezzo più rifrangente si avvicina alla normale, mentre un raggio luminoso che si rifrange da un mezzo più rifrangente a un mezzo meno rifrangente si allontana dalla normale.
Nella rifrazione si verifica il principio della reciprocità del cammino luminoso, cioè la luce, se proviene dal secondo mezzo incidendo con un angolo uguale ad r, si rifrange con un angolo uguale ad i; e se l'angolo di rifrazione diventa angolo di incidenza, quello di incidenza diventa angolo di rifrazione. Pertanto, indicando con n21 l'indice di rifrazione del primo mezzo rispetto al secondo, abbiamo che:
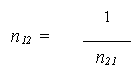
Se il raggio incidente è normale alla superficie di separazione dei due mezzi il raggio penetra nel secondo mezzo senza subire alcuna variazione di direzione, cioè, se l'angolo di incidenza è zero, anche quello di rifrazione è nullo.
L’indice di rifrazione assoluto di un mezzo è l'indice di rifrazione del mezzo considerato rispetto al vuoto. Gli indici di rifrazione assoluti dei vari mezzi sono maggiori dell'unità, quindi un raggio di luce che si rifrange dal vuoto a un mezzo si avvicina alla normale.
L'indice di rifrazione è il parametro fondamentale per caratterizzare un mezzo trasparente da un punto di vista ottico, due sostanze, pur essendo chimicamente diverse, sono invece otticamente identiche se presentano lo stesso indice di rifrazione.
Le leggi della rifrazione possono essere dedotte matematicamente, come le leggi della riflessione, dal principio di Fermat .
4.2 - Indici di rifrazione
Secondo la teoria ondulatoria, indicano con c la velocità di propagazione della luce nel vuoto e con v la velocità della luce in un mezzo trasparente qualsiasi, il cui indice di rifrazione assoluto sia n, abbiamo la seguente relazione:
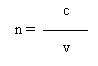
se il primo mezzo è il vuoto e se consideriamo due mezzi trasparenti 1 e 2, gli indici di rifrazione assoluti sono:
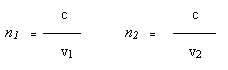
v1 e v2 sono le velocità di propagazione della luce rispettivamente nei mezzi 1 e 2.
Per cui abbiamo anche:
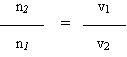
In base alle suddette relazioni possiamo scrivere la legge della rifrazione nel seguente modo:
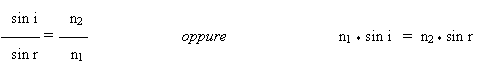
Per cui la relazione tra indice relativo e assoluto è: l'indice di rifrazione del mezzo 2 rispetto al mezzo 1 è uguale al rapporto fra l’indice di rifrazione assoluto del mezzo 2 e l’indice di rifrazione assoluto del mezzo 1:
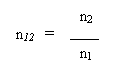
Da questa relazione deduciamo che, se n12>1 (n12 < 1), è n2> n1 (n2 <n1), cioè se il mezzo 2 è più rifrangente (meno rifrangente) del mezzo 1, l'indice di rifrazione assoluto del mezzo 2 è maggiore (minore) dell'indice di rifrazione assoluto del mezzo1
Gli indici di rifrazione dei vari mezzi sono maggiori dell'unità, per cui la velocità di propagazione della luce assume il valore massimo nel vuoto, e quanto più rifrangente è il mezzo, tanto minore è la velocità di propagazione della luce in esso.
Poiché l'indice di rifrazione assoluto del vetro è maggiore di quello dell'acqua, il vetro è più rifrangente dell'acqua, per cui un raggio di luce che passa dall'acqua al vetro si rifrange avvicinandosi alla normale alla superficie di separazione dei due mezzi nel punto dì incidenza.
La frequenza della luce non muta il processo di rifrazione. Così, se consideriamo, per esempio, un fascio luminoso che passa da un mezzo trasparente a un altro, unitamente alla direzione di propagazione mutano la velocità v e la lunghezza d'onda l in modo che il rapporto v/l rimane però sempre costante: rapporto che, come è noto, rappresenta la frequenza del fascio.
4.3 - Angolo limite e riflessione totale
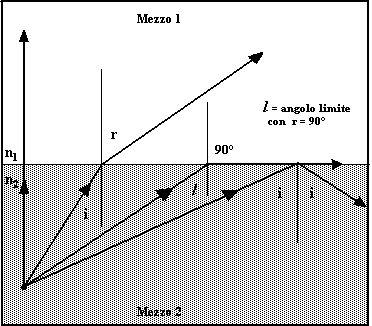
Quando i raggi che si rifrangono da un mezzo più rifrangente a un mezzo meno rifrangente si allontanano dalla normale, considerando successivamente angoli di incidenza sempre maggiori, si arriva a un particolare raggio con un angolo di incidenza tale che il raggio rifratto emerge radente la superficie di separazione dei due mezzi. In queste condizioni l'angolo di rifrazione è 90°, ed è detto angolo limite.
Ponendo n2 = n, r = l (angolo limite) e di conseguenza i =90°.
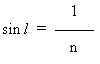
L'angolo limite è tale che il suo seno è uguale al reciproco dell'indice di rifrazione; perciò, conoscendo n, si può calcolare in definitiva l'angolo limite.
Se consideriamo un angolo di incidenza maggiore dell'angolo limite il seno dell'angolo di rifrazione, calcolato dovrebbe essere maggiore dell'unità, il che è impossibile. Questa situazione matematica corrisponde a un'impossibilità fisica del fenomeno della rifrazione; sperimentalmente infatti, quando l'angolo di incidenza è maggiore dell'angolo limite, non si ottiene alcun raggio rifratto. Il raggio di la luce in tali condizioni non passa nel secondo mezzo, ma viene riflesso dalla superficie di separazione dei mezzi, si ha la riflessione totale. Tutta l'energia associata al raggio incidente si trova integralmente (trascurando fenomeni di assorbimento) nel raggio riflesso.
In questo caso la superficie di separazione dei due mezzi trasparenti si comporta come uno specchio perfetto.
La riflessione totale può avvenire solo se la luce si propaga da un mezzo più rifrangente a un mezzo meno rifrangente, mentre non può in alcun caso avvenire se la luce va da un mezzo meno rifrangente a un mezzo più rifrangente.
4.4 - Diottro piano
Il diottro piano è un sistema di rifrazione formato da due mezzi aventi indice di rifrazione diverso e con superficie di separazione piana.
Nel diottro piano tutti i raggi che arrivano sulla superficie di separazione si rifrangono con lo stesso angolo, avvicinandosi alla normale se n1<n2 o allontanandosi dalla normale se n1>n2, e rimangono paralleli tra loro, senza subire alcuna convergenza o divergenza.
Vedremo più avanti la formula dei punti coniugati nel diottro piano.
Casi particolari di diottri piani sono: la lastra a facce parallele e il prisma ottico.
Lastra a facce piane e parallele
In una lastra a facce piane e parallele, mezzo trasparente con indice di rifrazione n2 immerso in un altro mezzo trasparente avente l'indice di rifrazione n1 con n2 > n1, un raggio luminoso che arriva sulla sua superficie piana si rifrange avvicinandosi alla normale. Il raggio rifratto incontra la seconda faccia della lastra con un angolo di incidenza e si rifrange nuovamente, però allontanandosi dalla normale. L'angolo di emergenza è uguale all'angolo di incidenza e il raggio emergente risulta parallelo al raggio incidente.
Quindi un raggio di luce che attraversa una lastra a facce piane e parallele non subisce alcuna variazione di direzione, ma viene spostato invece parallelamente al raggio incidente di un valore dato dalla seguente:
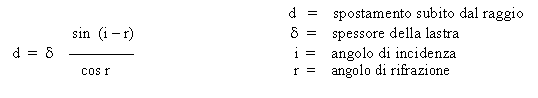
Quindi a parità di angolo di incidenza i lo spostamento subito dal raggio luminoso diminuisce con lo spessore d della lastra. E’ possibile anche dimostrare in modo analogo che un raggio di luce che attraversa più lastre a facce piane e parallele, se tutte le lastre si trovano nello stesso mezzo, esce dal sistema di lastre con la stessa direzione del raggio incidente, ma spostato parallelamente a se stesso.

Prisma ottico
Il prisma ottico è un mezzo trasparente limitato da due facce piane e non parallele. L'angolo a formato da queste due facce è detto angolo di rifrangenza del prisma. Se il prisma è più rifrangente del mezzo in cui si trova immerso, un raggio di luce, che penetra attraverso la prima faccia, si rifrange avvicinandosi alla normale. Questo raggio rifratto arriva poi sulla seconda faccia del prisma ed esce dal prisma allontanandosi dalla normale, se l'angolo che forma con la normale nel punto di incidenza è minore dell'angolo limite.
Indicando i l’angolo di incidenza, con e l'angolo formato dal raggio uscente dal prisma con la normale, detto angolo emergente, e con d quello formato dal raggio emergente con la direzione del raggio incidente, detto angolo di deviazione (deviazione complessiva subita dal raggio nelle due rifrazioni) possiamo scrivere le seguenti relazioni:
d = i + e - a se i = e allora d = 2i - a
Con la rifrazione attraverso un prisma permette è possibile determinare l'indice di rifrazione del mezzo considerato, se è noto l'angolo rifrangente a e l'angolo di deviazione minima dm :
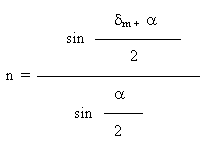
L’unità di misura della deviazione dei raggi luminosi prodotta da un prisma è la diottria prismatica “D” . Ha il potere di 1D un prisma che determina la deviazione di 1 cm un raggio luminoso su un piano situato a 1 m di distanza. Se il piano è situato a 2 m un prisma di 1D devia il raggio luminoso di 2 cm, se è a 3 m di 3cm, e così via. Un prisma di 3D determina uno spostamento di un raggio luminoso di 3 cm a 1 m.
Una diottria prismatica equivale a 0.57° di deviazione, mentre un grado è uguale a 1,75D.
Dispersione della luce
La separazione delle varie componenti cromatiche di base della luce bianca (policromatica) è detta dispersione della luce; può essere ottenuta facendo passare un sottile pennello di luce bianca, proveniente per esempio dal Sole o da una lampadina, attraverso un prisma di vetro. La luce, dopo aver attraversato il prisma ed essersi raccolta sullo schermo, evidenzia le componenti monocromatiche (rosso, arancione, giallo, verde, azzurro, indaco e violetto).
La composizione policromatica della luce bianca viene confermata anche dall’esperimento del disco colorato ruotante: prendiamo un disco contenente i colori fondamentali diviso in sette settori e facciamolo ruotare rapidamente intorno a un asse passante per il centro, il disco tende ad assumere un colore bianco in quanto, per la persistenza delle immagini sulla retina, i colori si sovrappongono.
I colori ottenuti dalla luce bianca non sono ulteriormente scomponibili. Se facciamo passare un raggio monocromatico dello spettro attraverso un prisma non si ottiene più un'ulteriore scomposizione.
Come è possibile spiegare la dispersione della luce in base alle leggi della rifrazione?
L'angolo di incidenza delle varie componenti cromatiche è unico, ma quello di rifrazione varia col colore. Questo dipende dal fatto che l'indice di rifrazione della luce varia quindi con la componente monocromatica considerata, ossia con il colore; l'indice di rifrazione assume valore minimo per il rosso e valori sempre maggiori man mano che si va verso il violetto, per cui l'angolo di rifrazione diminuisce dal rosso al violetto.
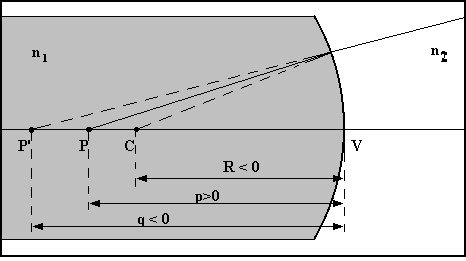
4.5 - Diottro sferico
Il diottro sferico è un sistema ottico costituito da due mezzi trasparenti omogenei con diverso indice di rifrazione n1 ed n2, separati da una superficie sferica di raggio di curvatura R e di centro C.
La superficie sferica può rivolgere alla sorgente luminosa la convessità o la concavità, quindi parliamo di diottro sferico convesso o diottro sferico concavo.
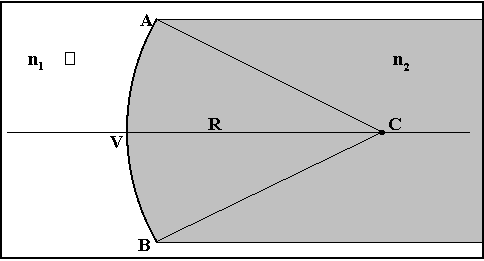
Elementi caratteristici
Come per gli specchi sferici, il diottro presenta i seguenti elementi:
1) angolo di apertura;
2) asse ottico principale: asse di simmetria, passante per il centro di curvatura C della superficie di separazione dei due mezzi;
3) vertice: punto di intersezione V dell'asse ottico con la calotta sferica;
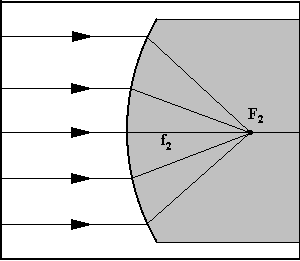
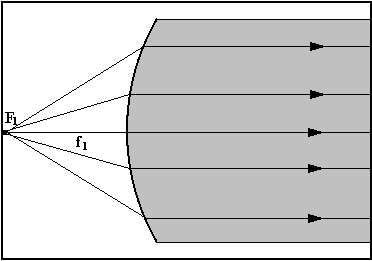
4) fuochi F1 ed F2: il primo fuoco F1 è il punto in cui , ponendo la sorgente puntiforme, i raggi rifratti proseguono paralleli all’asse; il secondo fuoco F2 è il punto in cui convergono, dopo la rifrazione, i raggi paralleli all’asse, cioè provenienti da una sorgente posta all’infinito.
5) distanze focali f1 ed f2: sono rispettivamente le distanze del primo e del secondo fuoco dal vertice.
Equazione dei punti coniugati
Un fascio di raggi uscenti da un punto oggetto P determina, dopo la rifrazione attraverso un diottro sferico, un fascio di raggi convergenti in un punto P’, oppure divergenti con i prolungamenti geometrici convergenti in un punto P’: nel primo caso diremo che P’ è immagine reale di P, mentre nel secondo caso diremo che P’ è immagine virtuale di P.
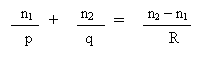
La precedente è l'equazione dei punti coniugati del diottro sferico (in base alle approssimazioni di Gauss).

Nelle precedenti relazioni se n2> n1 il segno di f1 ed f2 dipende esclusivamente da quello di R. Se entrambe le distanze focali sono positive e quindi entrambi i fuochi sono reali il diottro è convergente.
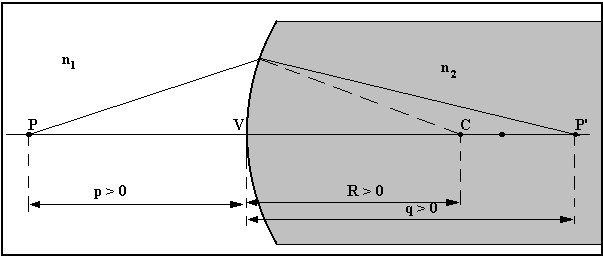
Potere diottrico
Il potere diottrico o anche potenza del diottro. è indicato dalla lettera D ed è dato da:
Esprimendo f1, f2 ed R in metri, la dimensione del potere diottrico, uguale all'inverso di una lunghezza, viene espresso in diottrie.
Un diottro è convergente quando D è positivo, mentre è divergente (fuochi virtuali) se D è negativo. Se il primo mezzo trasparente è l'aria, approssimando n1 = 1 (altrimenti sarebbe 1,000294), il potere diottrico può essere espresso dall'inverso della prima distanza focale:
D = 1 / f1
Il potere diottrico può essere anche chiamato potere convergente, perché il suo valore può rappresentare una misura della capacità del diottro di far convergere verso l'asse i raggi rifratti o i loro prolungamenti: più grande è il potere diottrico, più vicino si formano le immagini.
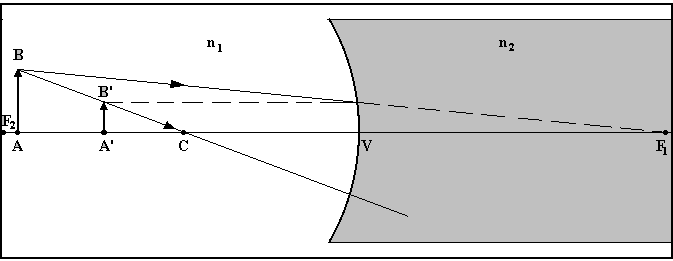
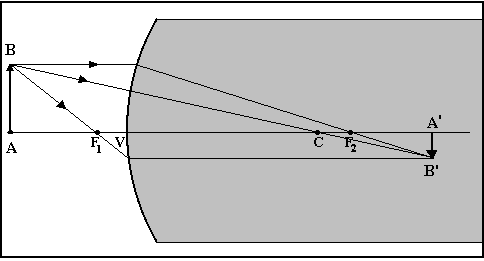
Costruzione delle immagini
La costruzione grafica dell'immagine di un oggetto si ottiene facilmente se sono note le posizioni del centro di curvatura e di uno dei due fuochi, o di tutti e due i fuochi. Infatti, i raggi che passano per il primo fuoco proseguono nel secondo mezzo parallelamente all'asse principale, i raggi che penetrano nel diottro parallelamente all'asse convergono nel secondo mezzo in f2, i raggi diretti verso il centro di curvatura proseguono non deviati perché la sua direzione è normale alla superficie del diottro.
Diottro piano
Nell’equazione dei punti coniugati facendo tendere R all'infinito otteniamo come caso particolare, l'equazione dei punti coniugati di un diottro piano:
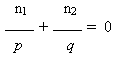
Essendo q < 0, il diottro piano abbiamo solo immagini virtuali di oggetti reali.
4.6 - Diottri sferici asimmetrici
I diottri sferici hanno le loro caratteristiche refrattive identiche e simmetriche in tutte le sezioni ortogonali dello spazio.
La simmetria può non essere uguale in tutte le sezioni per una differenza di curvatura tra due sezioni. In tal modo si avrà una differenza refrattiva tra le due sezioni.
Per esempio la sezione verticale può risultare più rifrangente e pertanto, attraverso il diottro nel suo complesso, l'immagine risulterà a fuoco non più sullo stesso piano e in un unico punto, ma su più piani e in uno spazio ampio in base alla differenza dei poteri diottrici delle due sezioni.
Un diottro sferico asimmetrico, considerato tridimensionalmente, presenterà infinite sezioni parallele tra loro, sia in senso orizzontale che in senso verticale, con caratteristiche refrattive proprie e con un suo punto focale; l’insieme dei punti focali formerà una linea orizzontale per tutte le sezioni verticali, mentre linea verticale sarà formata da tutte le sezioni orizzontali. Lo spazio compreso tra queste due linee e quello immediatamente circostante, visto tridimensionalmente, somiglia all’immagine di due coni collegati ed è detto Conoide di Sturm . Lo spazio compreso tra le due linee focali è l’intervallo di Sturm o spazio interfocale, che è tanto più ampio quanto maggiore è la differenza dei poteri rifrangenti delle due superfici.
Tra tutte le sezioni del conoide ne esiste una che ha forma circolare ed è detta “cerchio di minore diffusione o confusione”. Questo cerchio di minore diffusione o confusione, può considerarsi come il valore medio delle due distanze focali, il valore diottrico equivalente all'analogo diottro sferico simmetrico.
Diottro cilindrico
Il diottro cilindrico è un tipo di diottro asimmetrico, presenta una forma cilindrica con curvatura in un solo asse e determina una linea focale parallela all’asse longitudinale
Diottro torico
Il diottro torico è un altro tipo di diottro asimmetrico, ottenibile dalla rotazione di cerchi intorno ad assi non corrispondenti all'asse centrale ottenendo svariate forme con i seguenti nomi: barilotto, neumatica, , zucca, puleggia, ecc.
4.7 - Diottro composto
Il diottro composto è un sistema di mezzi trasparenti con diverse caratteristiche refrattive con i centri sulla stessa retta, ogni passaggio da un mezzo all’altro è un diottro che può essere considerato singolarmente e studiato con le leggi della diottrica. Tutti questi singoli diottri sono, in pratica, uniti a formare un diottro unico più complesso. Quindi il diottro composto è formato da due o più diottri semplici. La retta che unisce i centri è l'asse ottico del sistema.
In base alle leggi della rifrazione e dell’ottica geometrica e tenendo conto del potere rifrangente dei vari mezzi, è possibile costruire il decorso del dei raggi rifratti dal diottro d’ingresso a quello di uscita, anche se per i diottri più complessi è piuttosto difficile.
Il diottro composto centrato ha , anch’esso, due punti coniugati con l'infinito ( primo e secondo punto focale).
E’ possibile costruire l'immagine attraverso un diottro composto, basta tenere conto delle proprietà dei 6 punti cardinali (2 fuochi, 2 punti nodali, 2 punti principali) perché il meccanismo è molto simile a quello usato per il diottro semplice.
home page