| Ottica
oftalmica e fisiopatologia della refrazione Alfredo Parrozzani |
www.oculistanet.it |
5 - LE LENTI
Le lenti sono formate da un mezzo trasparente limitato da due superfici, delle quali almeno una di forma sferica; in pratica è formata da due diottri accoppiati, aventi i centri di curvatura sullo stesso asse. Se la distanza fra i vertici delle due calotte sferiche è trascurabile rispetto ai raggi di curvatura, la lente si dice sottile.
Le lenti si dividono in convergenti , più spesse al centro che ai bordi e con le due superfici convesse o quella con potere maggiore, e divergenti , più spesse ai bordi che al centro e con le due superfici concave o quella con potere maggiore. Questa regola è valida solo quando la lente si trova in un mezzo avente indice di rifrazione minore del materiale (generalmente vetro) di cui è fatta la lente; poiché generalmente una lente è immersa in aria, la regola può considerarsi assoluta.
5.1 - Caratteri fisici
Elementi di una lente
In una lente biconvessa (convergente) abbiamo come nel diottro, i seguenti elementi caratteristici:
1) C1, C2: centri di curvatura delle due calotte sferiche;
2) C1C2: asse ottico principale;
3) F1, F2: fuochi principali;
4) O: centro ottico; è il punto per il quale tutti i raggi che passano per esso corrispondono a coppie di raggi incidenti ed emergenti paralleli, in quanto la lente si comporta rispetto a questi raggi come una lastra;
5) s: asse secondario (qualsiasi retta passante per O);
6) F1’
, F2’; fuochi secondari7) ABCD: percorso geometrico di un generico raggio.
In una lente convergente i due fuochi principali F1 e F2 hanno le seguenti proprietà:
- i raggi uscenti da F1, dopo essersi rifratti nella lente, escono parallelamente all'asse ottico;
- i raggi paralleli all'asse ottico, dopo essere rifratti, escono convergendo nel secondo fuoco F2.

I fuochi situati su un asse secondario godono delle stesse proprietà. Nella lente convergente entrambi i fuochi sono reali.
In una lente divergente i due fuochi principali F1 e F2 hanno le seguenti proprietà:
- i raggi incidenti in direzione tale che i prolungamenti geometrici convergano nel fuoco F1, dopo essersi rifratti nella lente, escono parallelamente all'asse ottico;
- i raggi paralleli all'asse ottico, dopo essersi rifratti nella lente, escono divergendo in modo che i prolungamenti geometrici passino per il fuoco F2.
I fuochi situati su un asse secondario godono di proprietà analoghe. Nella lente divergente entrambi i fuochi sono virtuali.

Una lente può essere rappresentata schematicamente con un segmento verticale passante per il centro ottico e avente agli estremi due frecce: verso l’esterno nella lente convergente, verso l’interno in quella divergente.
Equazione dei punti coniugati
Le suddette proprietà del centro ottico e dei fuochi delle lenti, valgono solo per lenti sottili, nei limiti delle approssimazioni di Gauss, per raggi monocromatici poco inclinati rispetto all'asse ottico (raggi parassiali) e per diottri di piccola apertura.
L’equazione dei punti coniugati delle lenti sottili è calcolata applicando l'equazione dei punti coniugati di un diottro alle due facce della lente:
1/p + 1 /q = (n-1) (1/R1 - 1 /R2)
- n è l'indice di rifrazione della lente immersa in un mezzo con indice di rifrazione uguale all'unità;
- p e q sono le distanze del punto oggetto e del punto immagine dalla lente;
- R1 è il raggio di curvatura della prima calotta sferica, cioè quella di sinistra, è positivo o negativo a seconda che il centro si trovi nello spazio delle immagini reali o virtuali formate dal primo diottro, cioè a destra o a sinistra della prima faccia, nell'ipotesi ovviamente che la luce provenga da sinistra.;
- R2 è il raggio della seconda calotta, ossia quella posta a destra, rispetto alla quale l'immagine formata dal primo diottro si comporta come oggetto, per cui è positivo o negativo a seconda che il centro si trovi a destra o a sinistra della seconda faccia.
La relazione fra i punti coniugati, chiamata anche equazione degli ottici.
Così abbiamo:
·
R1 > 0 e R2 < 0 per una lente biconvessa;·
R1 > 0 e R2 > 0 con R1 < R2 per una lente menisco convergente;·
R1 <0 e R2 > 0 per una lente biconcava;·
R1 à infinito e R2 > 0 per una lente piano - concava .
Con l’equazione dei punti coniugati è possibile determinare la distanza q dalla lente dell'immagine di un punto di cui si conosce la distanza p dalla se noti i valori di n , R1 e R2.
Se poniamo p = f1, facendo tendere q all'infinito per il primo fuoco, e q = f2 , facendo tendere p all'infinito per il secondo fuoco, l’equazione dei punti coniugati si riduce a :
1/f1 + 1 /f2 = (n-1) (1/R1 - 1 /R2)
o anche nella forma:
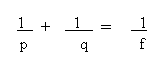
con
1/f = (n-1) (1/R1 - 1 /R2)
Nelle lenti f è nota come distanza focale, positiva per le lenti convergenti e negativa per le lenti divergenti. Quindi i fuochi sono reali per le lenti convergenti e virtuali per le lenti divergenti .
Se non teniamo conto delle approssimazioni di Gauss, di raggi luminosi monocromatici e provenienti da un oggetto puntiforme e non convergenti tutti in un unico punto, si ha una certa confusione nell'immagine, chiamata aberrazione .
Potere diottrico
La potenza di una lente è data dal potere diottrico, che è il reciproco della distanza focale:
D = 1/f
Il potere diottrico, avendo lo stesso segno della distanza focale, è positivo per le lenti convergenti e negativo per le lenti divergenti. Il potere diottrico si esprime in diottrie se la distanza focale viene espressa in metri.
Per esempio, una lente convergente di 5 diottrie ha la distanza focale di 20 cm, mentre una lente divergente di -10 diottrie ha la distanza focale a 10. Se un sistema ottico è formato da più lenti con lo stesso asse principale, il potere diottrico totale è uguale alla somma algebrica dei poteri diottrici di ogni lente del sistema.
Ingrandimento nelle lenti
Le dimensioni lineari dell'immagine sono diverse da quelle dell'oggetto, perciò può essere introdotta una nuova grandezza, chiamata ingrandimento lineare o trasversale e comunemente indicata con G. Questa grandezza rappresenta il rapporto tra la misura del segmento immagine e la misura del segmento oggetto:

Aberrazioni
Se non sono soddisfatte le condizioni ideali come sorgenti luminose monocromatiche, sistemi ottici di piccola apertura e raggi incidenti e rifratti parassiali, le immagini risultano piuttosto sfumate, confuse, distorte, e la loro forma geometrica non corrisponde più a quella dell'oggetto.
Queste alterazioni dell’immagine sono chiamate aberrazioni, che non dipendono dalle imperfezioni tecniche e costruttive dei sistemi ottici, ma sono connessi con la rifrazione della luce attraverso le superfici curve delle lenti.
Aberrazione cromatica
Si ha se la sorgente luminosa non è monocromatica. La distanza focale di una lente è legata al proprio indice di rifrazione; poiché quest'ultimo varia al variare della lunghezza d'onda (dispersione), anche la distanza focale viene a dipendere dalle lunghezze d'onda che compaiono in un fascio policromatico.
Quindi quando la luce, proveniente da una sorgente puntiforme non monocromatica, attraversa una lente, anche il potere convergente o divergente del sistema diottrico dipende dalla lunghezza d'onda. La convergenza è più elevata per i raggi violetti di piccola lunghezza d'onda, che così risultano più deviati, mentre è più ridotta per le radiazioni corrispondenti al rosso. Così si forma una serie di immagini puntiformi, ognuna delle quali corrisponde a una componente monocromatica del fascio, in tal modo l'immagine presenta i bordi colorati.
E’ possibile ridurre o eliminare l’aberrazione cromatica con lenti direttamente di natura e di convergenza diversa, scelte in modo da compensare le imperfezioni cromatiche introdotte da ogni singola lente del sistema.
Aberrazione sferica
Viene provocata da un fronte d'onda piuttosto esteso che attraversa un sistema ottico la cui apertura non soddisfa le condizioni dì Gauss.
Il potere convergente o divergente di una lente non risulta più costante: il valore è uguale per i raggi parassiali che arrivano nella zona centrale della lente ma varia entro certi limiti per i raggi marginali che colpiscono le porzioni periferiche del sistema. In questi raggi le componenti più esterne sono focalizzate più vicino alla lente, mentre quelle più prossime all'asse tendono a focalizzarsi in punti più distanti.
La superficie formata dall'insieme dei raggi uscenti dalla lente è detta caustica di rifrazione. Per questo motivo si determinerà un’immagine non è perfetta, si formeranno correttamente solo alcune limitate porzioni dell'oggetto.
L'aberrazione di sfericità può essere ridotta combinando opportunamente più lenti fra loro e diaframmando il fascio affinché le radiazioni arrivino solo nella parte centrale della lente.
5.2 - Tipi di lenti
Lenti sferiche
Le lenti sferiche sono diottri simmetrici (doppio diottro) di cui almeno una delle due superfici ha la forma di una sezione più o meno ampia di sfera, l’altra superficie può essere anch’essa sferica o piana. Essendo sferica e regolare determina un fuoco teoricamente puntiforme, reale o virtuale. La superficie può essere concava, per cui la lente risulterà divergente, o convessa, realizzando una lente convergente. Questo tipo di lente è il più semplice ed è caratterizzato solo dal potere diottrico.
Le lenti sferiche possono essere:
|
Lente |
Prima superficie |
Seconda superficie |
Vergenza |
|
Piano - convessa |
convessa |
piana |
convergente |
|
Biconvessa |
convessa |
convessa |
convergente |
|
Concavo - convessa |
convessa |
concava |
converg. o diverg. |
|
Biconcava |
concava |
concava |
divergente |
|
Piano - concava |
piana |
concava |
divergente |
Lenti cilindriche
Le lenti cilindriche sono particolari diottri asimmetrici con forma cilindrica; in questi diottri la rifrazione produce una linea focale parallela all’asse del cilindro. Perciò un cilindro, disposto verticalmente, determina una linea focale verticale (reale se positivo, virtuale se negativo), mentre un cilindro, disposto orizzontalmente, determina una linea focale orizzontale. Le lenti cilindriche sono caratterizzate dal potere diottrico e da un asse, nella cui direzione il potere è nullo, perpendicolare alla direzione del potere massimo. Negli assi intermedi il potere varia tra 0 e il potere massimo della lente.
Unendo due cilindri con assi ortogonali abbiamo un diottro bicilindrico simile al diottro sferico asimmetrico; se i due cilindri ortogonali sono identici il diottro risultante equivale a un diottro sferico simmetrico. Di conseguenza qualsiasi diottro sferico asimmetrico può essere scomposto in due diottri cilindrici uguali con assi ortogonali.
Le lenti cilindriche possono avere, nella direzione ortogonale all’asse, le stesse caratteristiche delle lenti sferiche (vedi tabella delle lenti sferiche), inoltre possono essere semplici o composte:
|
Lente cilindrica semplice convessa |
convergente |
positiva |
una linea focale |
|
Lente cilindrica semplice concava |
divergente |
negativa |
una linea focale |
|
Lente cilindrica composta sfero-cilindrica convessa |
convergente |
positiva |
due linee focali con conoide |
|
Lente cilindrica composta sfero-cilindrica concava |
divergente |
negativa |
due linee focali con conoinde |
Lenti toriche
Le lenti toriche diottri torici e sono caratterizzate da una combinazione di superfici a diverso potere diottrico, in tal modo è possibile avere poteri molto diversi, addirittura opposti nelle varie zone della lente. Queste lenti vengono molto usate nella pratica costruttiva delle lenti correttive per le loro caratteristiche e per la maggiore praticità di realizzazione rispetto ad altri tipi di lenti.
home page